Section 3.二分法

一、二分的本质

• 在一个序列中，存在某种性质，使得该序列可以一分为二，使左半边满足这种性质，右半边不满足这种性质，二分可以寻找这种性质的边界
• 常用于边界问题

二、整数二分的过程

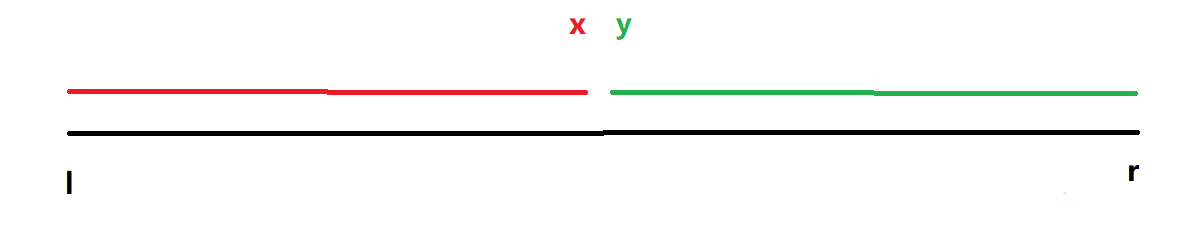
• 当我们想二分找出 x 点时

1. 找到一个中间值 d=(l+r+1)/2 ，判断这个点的性质是否具有左半边性质（ l+r+1 的原因是下面的更新方式是 l=mid ）
2. 如果具有，则真正的边界可能在 [mid,r] 中（之后的更新方式： l=mid ），否则真正的边界可能在 [l,mid-1] 中（之后的更新方式： r=mid-1 ）

int dichotomy(int l, int r)
{
	while (l < r)
	{
		int mid = l + r + 1 >> 1;  //因为下面的更新方式是l=mid
		if (check(mid)) //check函数为判断是否符合左边性质
			l = mid;  //答案在mid右边
		else r = mid - 1;  //答案在mid左边（不包括mid因为check为否）
	}
	return l;  //循环结束条件为l==r所以返回l或r都行
}

• 当我们想二分找出y点时

1. 找到一个中间值 mid=(l+r)/2 ，判断这个点的性质是否具有右半边性质
2. 如果具有，则真正的边界可能在 [l,mid] 中（之后的更新方式： r=mid ），否则真正的边界可能在 [mid+1,r] 中（之后的更新方式： l=mid+1 ）

int dichotomy(int l, int r)
{
	while (l < r)
	{
		int mid = l + r >> 1;
		if (check(mid))  //check函数为判断是否符合右边性质
			r = mid;  //答案在mid左边
		else l = mid + 1;  //答案在mid右边（不包括mid因为check为否）
	}
	return l;  //循环结束条件为l==r所以返回l或r都行
}

三、浮点数二分的过程

• 浮点数二分非常简单，因为不需要考虑边界问题，原理和整数二分相同

double dichotomy(double l, double r)
{
	while (r - l < x)  //x为精度，取决于题目的要求
	{
		double mid = (l + r) / 2;
		if (check(mid))
			r = mid;  //答案在mid左边
		else l = mid;  //答案在mid右边
	}
	return l;  //l和r都行
}

四、配套练习

AcWing789

AcWing790