一、暴力求解!
string s, p; //长度为n的模式串s和长度为m的模版串p
for (int i = 1; i <= n; i++)
{
bool flag = true;
for (int j = 1; j <= m; j++)
{
if (s[i - j + 1] != p[j])
{
flag = false;
break;
}
}
}
Time Limit Error 警告 !
二、优雅地求解
- 前缀和后缀、同一个串的前缀和后缀相同部分的最大长度(下文简称公共最大长)
- 前缀:在一个串中,包含第一个元素且不包含最后一个元素的子串
qwerwq的前缀:q、qw、qwe、qwer、qwerw
qweqw的前缀:q、qw、qwe、qweq
- 后缀:在一个串中,包含最后一个元素且不包含第一个元素的子串
qwerwq的后缀:q、wq、rwq、erwq、werwq
qweqw的后缀:w、qw、eqw、weqw
- 公共最大长
qwerwq的公共最大长: 1
qweqw的公共最大长: 2
- 利用公共最大长对模式串匹配进行优化

max数组为从模版串头部到当前位置的公共最大长next数组为max - 1
现在,我们假设匹配时有以下情况:
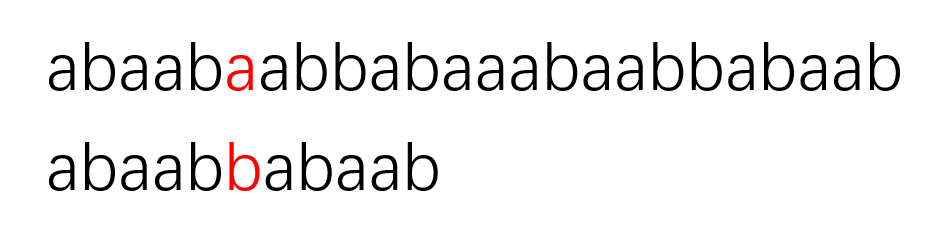
如上图所示,模版串在第六个字符处(下标 5 )配对失败,此时我们可以确认的是前面五个字符已经配对成功了,我们根据上面的表格查找一下已经匹配成功的部分的公共最大长(第五个字符对应的 max 值,max[4] )。很明显,已经匹配成功的部分的公共最大长为 2 ,这说明了什么?配对成功的部分的前两个字符和后两个字符是相同的,这也就意味着我们重新进行匹配的时候可以将模版串头部的两个字符和模式串匹配成功的最后两个字符对齐,然后开始比较模版串的第三个字符和模式串中配对失败的字符,开始新一轮匹配
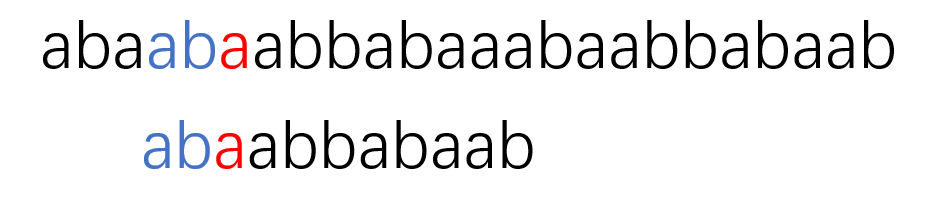
我们如何实现上图中对齐的过程?我们在匹配时分别用指针 i 和 j 指向字符串当前匹配的位置,匹配失败后指针 i 不变,继续指向模式串匹配失败的地方,而指针 j 则指向模版串的第三个位置。我们发现,第三个位置刚好是之前已经配对完成的部分的公共最大长 (2) 的后面一位,这个位置对应的下标则刚好是之前已经配对完成的部分的公共最大长!
那么问题来了:我们如何求出next数组?总不可能靠手算吧?
max(next)数组的求解
首先,next 数组是什么?正如表示公共最大长的 max 数组的值正好同时表示了对应的最大前缀的后面一位的数组下标(为了方便表示,我们将 前缀中前缀和后缀的最大相同部分称为最大前缀,最大后缀同理 ),next 数组中的值等于 max 数组中的值减去 1 ,那么 next 数组可以用来表示对应的最大前缀的最后一位的数组下标。下面,我们讨论对 next 数组求解。
我们可以知道模版串的第一个字符对应的最大公共长一定是 0 ,它对应的 next 则为 -1 ,所以next[0] = -1 ,接下来,我们不从第二个字符开始类推,而是选取一个位置靠后的具有普适性的例子以便更好地理解推导过程。如下图所示:

假设我们已经一步步推导得出了前面 0 \sim 9 下标对应的 next 值,现在要求求出下标 10 对应的 next 值( 公共最大长 - 1 )。
我们首先需要考虑添加了字符 b 之后的公共最大长是否会增加 1 ,该如何判断呢?
将下标 10 对应的字符和前面已经求得解的最长字符串 abaabbabaa 的最大前缀的后面一个字符比较,如果二者相同,说明了最大前缀往后添加一位后产生的字符串和最大后缀添加了字符 b 产生的字符串相同,此时下标 10 对应的公共最大长应该在前面一位的基础上加一。
那么这个字符串 abaabbabaa 的最大前缀的后一位的下标值怎么求?
这个值是已经求得解的最长字符串的公共最大长的值,即为 max[9] ,或者说 next[9] + 1。( max[9] 对应了公共最大长的值,也表示着最大前缀后一位的下标)
这个值具体是什么?
是 next[9] + 1 = 3 + 1 = 4。我们继续寻找下标 4 对应的字符,是 b ,和下标 10 对应的字符相同,所以下标 10 对应的公共最大长相较之前一位加一, new 值加一,所以 new[10] = new[9] + 1 = 3 + 1 = 4。
可是,如果模版串下标10对应的不是'b'呢,如下图,是'a'呢?怎么办?

很明显,按照之前的推理,在当前情况下,模版串[10] = 'a'和模版串[4] = 'b'是不等的,所以最大公共长不可能增加了,我们只能考虑其与前一位相等甚至减少的情况了,此时该怎么求呢?我们现在要找的是 最大前缀的前缀 ,与"最大后缀加上一个a字符”的后缀的公共最大长了,此时我们要求解的问题其实转化成了 下标 0 \sim 9 的最大前后缀后面添加一个字符a 对应的公共最大长,于是我们先利用下标 10 前面一位下标 9 对应的 next 的值找到下标 0 \sim 9 的最大前缀的最后一位,并重复上面的过程来推测此时公共最大长应该朝什么方向变化,如果向前找到的最后一位的next值是-1,即最大公共长已经减到0的时候,循环终止。如果这两句话没有理解,可以先看看代码,对应上表理解:
//数组B是模版串
next[0] = -1;
for (int i = 1; i < n; i++) //n为模版串长度
{
int j = next[i - 1]; //j为待计算位置前一位对应的next值,也就是最大前缀最后一位对应的索引
while (B[j + 1] != B[i] && j >= 0) //任何一个最大前缀后一位与当前求值字符相同时或者向前继续寻找的索引为-1时停止循环
j = next[j];
if (B[j + 1] == B[i]) //字符相同,公共最大长+1,next值+1
next[i] = j + 1;
else //最终寻找到的索引为-1,公共最大长归零
next[i] = -1;
}
我们终于求完 next 数组了,结合前文中对齐的过程, 我们直接看代码中的注释:
for (int i = 0, j = -1; i < m; i++) //如同求next数组,j为待计算位置前一位的next值
{
while (j >= 0 && S[i] != B[j + 1]) //j+1是最大前缀的后一位的下标
j = next[j];
if (S[i] == B[j + 1])
j++;
if (j + 1 == n)
{
//此处是匹配成功一次的位置,可以进行某些输出操作
//cout << i - n + 1 << " ";
j = next[j];
}
}
下面给出完整代码:
#include <iostream>
using namespace std;
int main()
{
int n, m;
char B[100010], S[1000010];
int next[100010];
next[0] = -1;
cin >> n >> B >> m >> S;
for (int i = 1; i < n; i++)
{
int j = next[i - 1];
while ((B[j + 1] != B[i]) && (j >= 0))
{
j = next[j];
}
if (B[j + 1] == B[i])
next[i] = j + 1;
else
next[i] = -1;
}
for (int i = 0, j = -1; i < m; i++)
{
while (j >= 0 && S[i] != B[j + 1])
j = next[j];
if (S[i] == B[j + 1])
j++;
if (j + 1 == n)
{
//此处是匹配成功一次的位置,可以进行某些输出操作
//cout << i - n + 1 << " ";
j = next[j];
}
}
return 0;
}
