一、DFS与BFS的原理
有请我们的五毛钱特效!
DFS
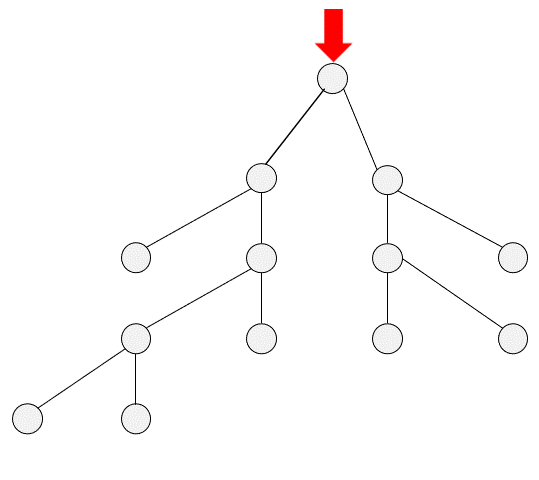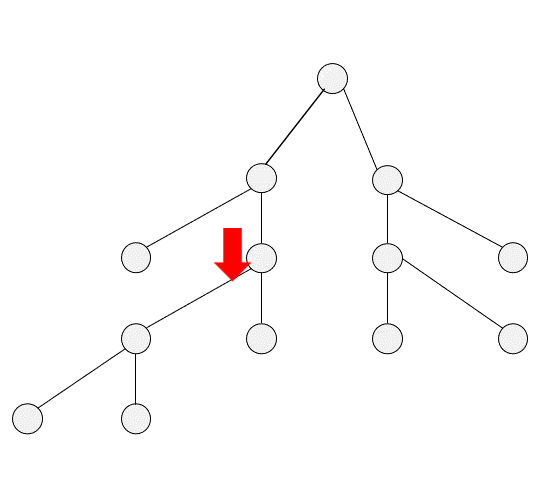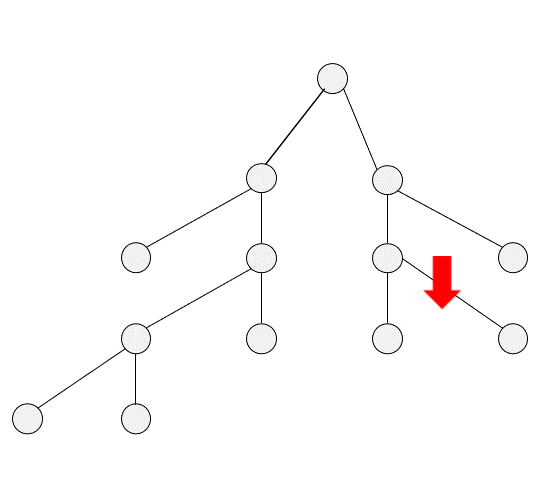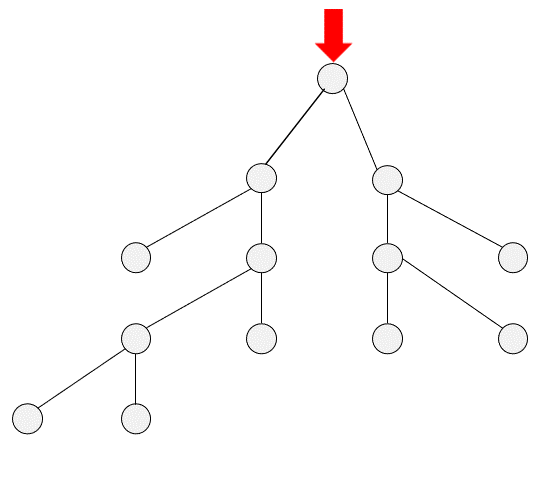
BFS
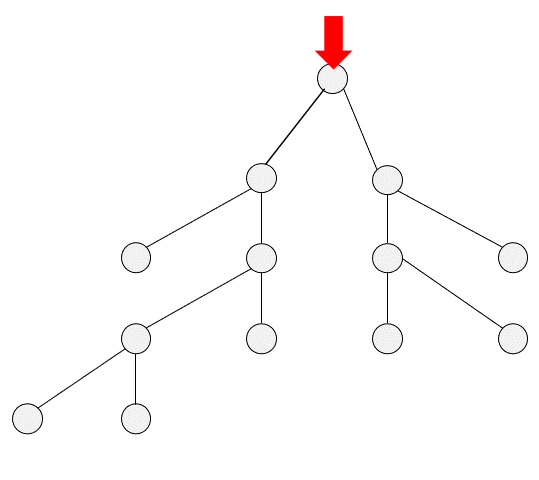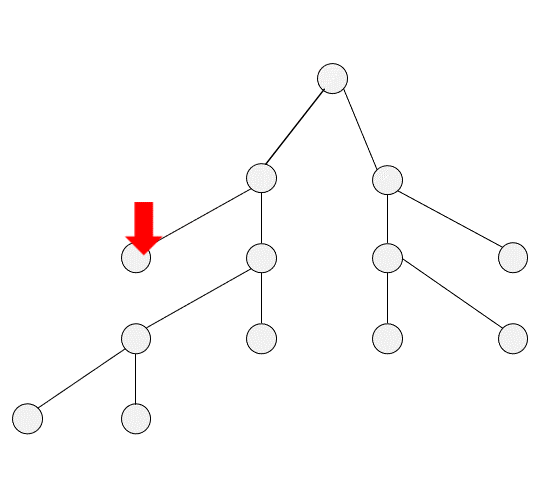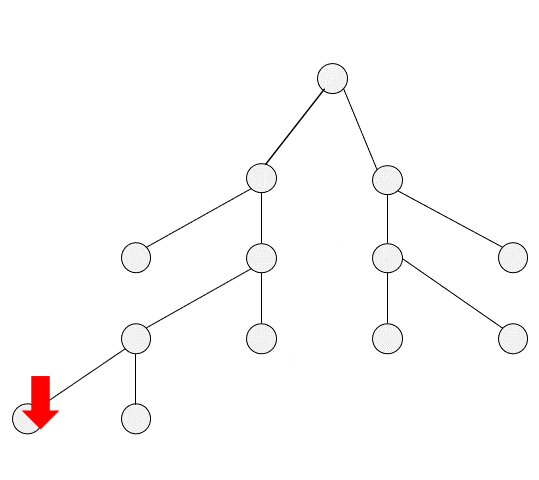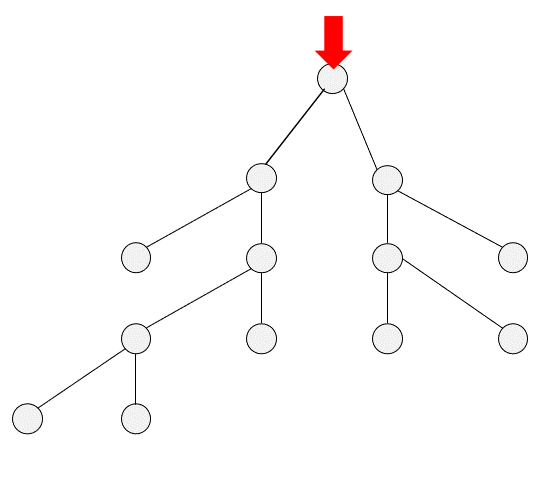
二、DFS的实现
#include <iostream>
using namespace std;
const int N = 10;
int n;
int path[N]; //存储路径,DFS只存储当前路径
bool st[N]; //用来存储当前这个数有没有被用过
void dfs(int u) //参数表示层数,判断第一个数字是第0层
{
if (u == n) //已经遍历到当前支的最后一个节点
{
for (int i = 0; i < n; i++)
printf("%d ", path[i]);
printf("\n");
return;
}
for (int i = 1; i <= n; i++)
{
if (!st[i]) //数i没有被用过
{
path[u] = i; //该层放置数字i
st[i] = true; //标记为已用
dfs(u + 1); //判断下一层
st[i] = false; //还原这一层的数字使用状态,因为即将退回上一层
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}
#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N]; //一组方案
bool col[N]; //用来存用过的列,用过了就不能再用了
bool dg[N]; //用来存用过的对角线
bool udg[N]; //用来存用过的反对角线
void dfs(int u)
{
if (u == n) //找到了一组方案
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
cout << g[i][j];
cout << endl;
}
cout << endl;
return;
}
for (int i = 0; i < n; i++) //枚举第u行皇后放在哪一列
{
if (!col[i] && !dg[u + i] && !udg[n - u + i]) //第u行第i列上的反对角线截距为i+u,对角线截距为i-u,因为数组下标不可能小于0,所以统一+n
{
g[u][i] = 'Q';
col[i] = dg[i + u] = udg[i - u + n] = true;
dfs(u + 1);
col[i] = dg[i + u] = udg[i - u + n] = false;
g[u][i] = '.';
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
g[i][j] = '.';
dfs(0);
return 0;
}
三、BFS的实现
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef pair<int, int>PII;
const int N = 110;
int n, m;
int g[N][N]; //用来存地图(01)
int d[N][N]; //到起点的距离
PII q[N * N];
int bfs(void)
{
int hh = 0, tt = 0; //队头、队尾
q[0] = { 0,0 };
memset(d, -1, sizeof d); //初始化距离为-1
d[0][0] = 0;
int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 }; //dx横坐标,dy纵坐标
while (hh <= tt) //当队列非空时
{
auto t = q[hh++]; //取出队头元素
for (int i = 0; i < 4; i++)
{
int x = t.first + dx[i];
int y = t.second + dy[i]; //4次分别进行上移下移左移右移
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) //如果这个点在边界以内且可以走且没有走过
{
d[x][y] = d[t.first][t.second] + 1; //这个点的距离等于上一个点的距离+1
q[++tt] = { x,y }; //加入队列
}
}
}
return d[n - 1][m - 1]; //输出右下角的点(终点)的距离
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
cin >> g[i][j];
}
}
cout << bfs() << endl;
return 0;
}
使用STL容器queue队列的版本:
#include <iostream> #include <algorithm> #include <cstring> #include <queue> using namespace std; typedef pair<int, int>PII; const int N = 110; int n, m; int g[N][N]; //用来存地图(01) int d[N][N]; //到起点的距离 queue<PII> q; int bfs(void) { q.push({ 0,0 }); //插入第一个元素(起点) memset(d, -1, sizeof d); //初始化距离为-1 d[0][0] = 0; int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 }; //dx横坐标,dy纵坐标 while (!q.empty()) //当队列非空时 { auto t = q.front(); //读取队头元素 q.pop(); //弹出队头元素 for (int i = 0; i < 4; i++) { int x = t.first + dx[i]; int y = t.second + dy[i]; //4次分别进行上移下移左移右移 if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) //如果这个点在边界以内且可以走且没有走过 { d[x][y] = d[t.first][t.second] + 1; //这个点的距离等于上一个点的距离+1 q.push({ x, y }); //加入队列 } } } return d[n - 1][m - 1]; //输出右下角的点(终点)的距离 } int main() { cin >> n >> m; for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { cin >> g[i][j]; } } cout << bfs() << endl; return 0; }
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;
int bfs(string state)
{
queue<string> q;
unordered_map<string, int> d; //每种状态用排列方式的哈希值来表示
q.push(state);
d[state] = 0; //初始状态距离为0
int dx[4] = { -1, 0, 1, 0 }, dy[4] = { 0, 1, 0, -1 };
string end = "12345678x"; //结束状态
while (!q.empty())
{
auto t = q.front();
q.pop();
if (t == end) //如果到达了结束状态
return d[t];
int distance = d[t];
int k = t.find('x'); //x在一维数组中的位置
int x = k / 3, y = k % 3; //将一维坐标转换成二维坐标
for (int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3) //如果在边界内
{
swap(t[a * 3 + b], t[k]); //将(a,b)转换成一维坐标
if (!d.count(t)) //如果这个状态没有出现过
{
d[t] = distance + 1;
q.push(t);
}
swap(t[a * 3 + b], t[k]); //还原
}
}
}
return -1; //只有无解才会到这一步
}
int main()
{
char s[2];
string state;
for (int i = 0; i < 9; i++)
{
cin >> s;
state += *s;
}
cout << bfs(state) << endl;
return 0;
}
