差分约束

_{部分内容来自差分约束 - 知乎}

一、简介

差分约束系统是一种多元一次不等式组（ y_1,\ y_2 ,...,y_n 为已知量）：

其中，每个不等式称为一个约束条件，都是两个未知量之差小于等于某个常数。

很多题目会给出（或隐性地给出）一系列的不等关系，我们可以尝试把它们转化为差分约束系统来解决。

二、中心思想

我们设 $x_1-x_2\le c$，移项可得 $x_1\le x_2 + c$。

观察这个不等式与最短路问题中的三角形不等式 $\text{dist}[u]\le \text{dist}[v]+w_{v,u}$ 的相似之处，可以发现，我们可以把它转化为一个图论问题。也就是说，对于每一个 $x_{c_i}-x_{c_i'}\le y_i$，我们都从 $c_i'$ 到 $c_i$ 建一条边，边权为$y_i$.

这样建出的有向图，它的每个顶点都对应差分约束系统中的一个未知量，源点到每个顶点的最短路对应这些未知量的值，而每条边对应一个约束条件。

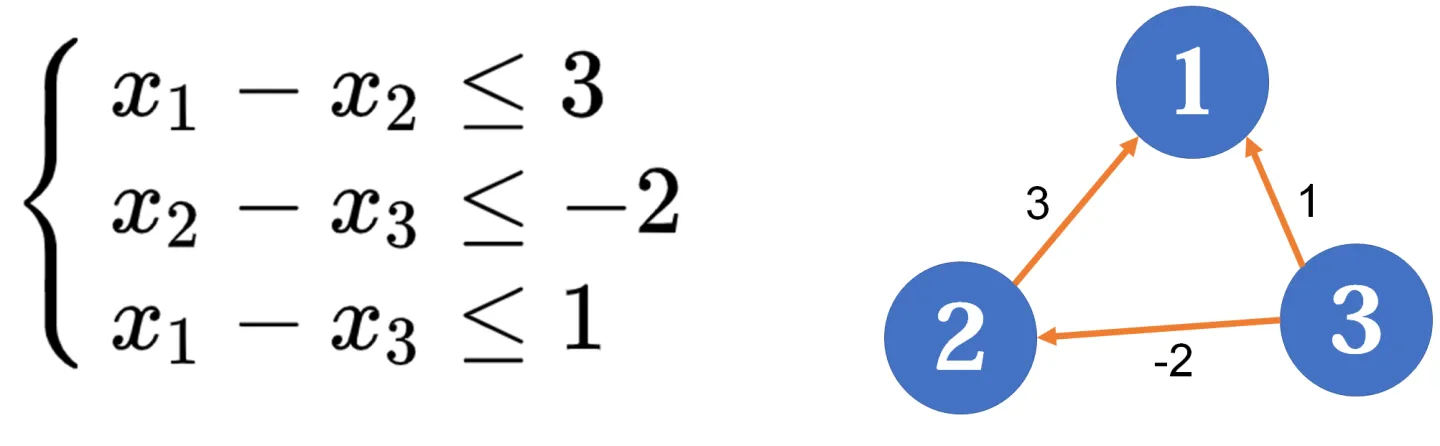
既然是最短路，那么我们应该选取哪个点作为源点？事实上，选取哪个点作为源点是无关紧要的。但是，我们得到的图不一定是连通的，为了避免出现结果为 $INF$ 的情况，我们可以人为增加一个超级源点。

例如，我们现在人为新增一个 $0$ 号点，从它向所有顶点连一条遍权为 $0$ 的边：

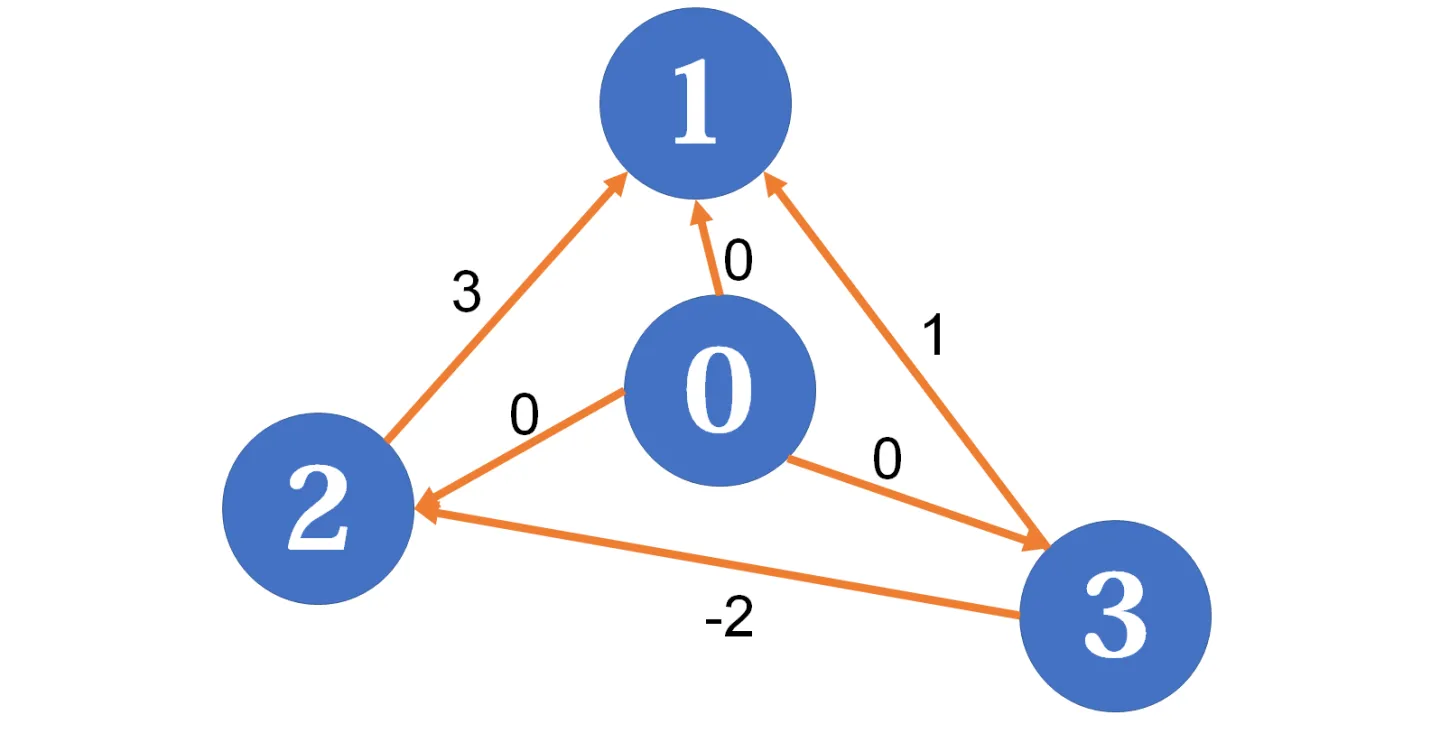
现在我们以$0$号点为源点求最短路即可。注意，这相当于添加了以下约束条件：

$$\begin{cases}x_1-x_0\le 0\\x_2-x_0\le 0\\x_3-x_0\le 0\end{cases}$$

由于 $x[0]$ 对应的是 $dist[0]$ ，而 $dist[0] = 0$ ，可知所有未知量均小于等于0（反映在图形上是所有点的最短路均小于等于0）。但实际上我们往往要的是非负解。根据简单线性代数原理可知，在符合差分约束系统的一组解上加上或减去同一个数，得到的解同样符合原系统。例如，上文例子求得的结果为 $x_1 = 0, x_2=−2, x_3=0$ ，然而 $x_1 = 2, x_2 = 0, x_3 = 2$ 也是一组解。

我们可以把 $dist[0]$ 设为另一个数 $w$ 而不是 $0$（或者把从0号点连向各点的边权设为 $w$ ），那么我们得到的便是满足 $x_1, x_2, ..., x_n \le w$的一组解。实际上，可以证明，它们是满足 $x_1, x_2, ..., x_n \le w$的最大解（每个变量取到能取到的最大值）：

假设约束系统存在解，我们知道，给定超级源点的一个偏移量 $d[0]$（即 $d[0]$不一定为 $0$），就能由最短路径树确定差分约束系统的一组解（树上两点间路径唯一确定）。同样的，给定最短路径树上任一个节点的值 $d[v]$，都可以求出超级源点的偏移量 $d[0]$，同样也确定了差分约束系统的一组解。对于从 $0$ 到 $v$ 的任意一条路径 $p(0,v1,v2,...,v_n)$，其所表示的约束式分别为： $x[v_1]-x[0] \le 0, \ x[v_2]-x[v_1] \le w(v_1,v_2), \ ..., \ x[v]-x[v_n] \le w(v_n,v)$。叠加得到 $x[v]-x[0] \le w(p)$，令 $x[0]$ 为确定值 $d[0]$，即 $x[v] \le d[0]+w(p)$， $p$为从 $0$ 到 $v$ 的任意路径。取 $p$ 为 $0$ 到 $v$ 的最短路 $p^*$，就有 $x[v] \le x[0]+w(p^*) \le x[0]+w(p)$。则当 $x[v]=d[0]+w(p^*)$时 $x[v]$取得最大值。

以上证明可能略显繁琐，以下给出一个不严谨的证明：考虑Bellman-Ford算法的过程，在差分约束系统中，假设 $X_0$ 是定死的， $X_1$到 $X_n$在满足所有约束的情况下可以取到的最大值分别为 $M_1,M_2,...,M_n$（当然我们不知道它们的值是多少），解出的源点到每个点的最短路径长度为 $D_1,D_2,...,D_n$。基本的Bellman-Ford算法是一开始初始化 $D_1$到 $D_n$都是无穷大，然后检查所有的边对应的三角形不等式，一但发现有不满足三角形不等式的情况，则更新对应的 $D$ 值。最后求出来的 $D_1$到 $D_n$就是源点到每个点的最短路径长度。如果我们一开始初始化 $D_1,D_2,...,D_n$的值分别为 $M_1,M_2,...,M_n$，则由于它们全都满足三角形不等式（我们刚才已经假设 $M_1$到 $M_n$是一组合法的解），则Bellman-Ford算法不会再更新任合 $D$值，则最后得出的解就是 $M_1,M_2,...,M_n$。可以发现，初始值无穷大时，算出来的是 $D_1,D_2,...,D_n$，初始值比较小时，算出来的则是 $M_1,M_2,...,M_n$。大家用的是同样的算法，同样的计算过程，总不可能初始值大的算出来的结果反而小吧。所以 $D_1,D_2,...,D_n$就是 $D_1,D_2,...,D_n$。

那么如何求满足 $x_1,x_2,...,x_n \ge w$ 的最小解呢？只需要求最长路就行了。最长路满足三角形不等式 $dist[u] \ge dist[v] + w_{v,u}$ ，所以相应的差分约束系统需要把小于等于符号换成大于等于符号。对于Bellman-Ford或SPFA算法来说，只需要初始化为 $-INF$ 而不是 $INF$，然后把比较符号颠倒一下即可。

三、例题

【模版】差分约束算法

题目描述

给出一组包含$m$ 个不等式，有$n$个未知数的形如：

$$ \begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases}$$

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数$n,m$ ,代表未知数的数量和不等式的数量。

接下来$m$行，每行包含三个整数$c,c',y$，代表一个不等式$x_c-x_{c'}\leq y$。

输出格式

一行， $n$个数，表示$x_1 , x_2 \cdots x_n$的一组可行解，如果有多组解，请输出任意一组，无解请输出NO。

样例 #1

样例输入 #1

3 3
1 2 3
2 3 -2
1 3 1

样例输出 #1

5 3 5

样例解释

$\begin{cases}x_1-x_2\leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases}$

一种可行的方法是$x_1 = 5, x_2 = 3, x_3 = 5$。

$\begin{cases}5-3 = 2\leq 3 \\ 3 - 5 = -2 \leq -2 \\ 5 - 5 = 0\leq 1 \end{cases}$

数据范围

对于$100\%$ 的数据，$1\leq n,m \leq 5\times 10^3$，$-10^4\leq y\leq 10^4$，$1\leq c,c'\leq n$，$c \neq c'$。

评分策略

你的答案符合该不等式组即可得分，请确保你的答案中的数据在 int 范围内。

如果并没有答案，而你的程序给出了答案，SPJ 会给出 There is no answer, but you gave it，结果为 WA；

如果并没有答案，而你的程序输出了 NO，SPJ 会给出 No answer，结果为 AC；

如果存在答案，而你的答案错误，SPJ 会给出 Wrong answer，结果为 WA；

如果存在答案，且你的答案正确，SPJ 会给出 The answer is correct，结果为 AC。

例程

import java.util.*;

public class Main {
    public static final int N = 5010;
    public static int index = 0;
    public static int[] h = new int[N];
    public static int[] dist = new int[N];
    public static List<Edge> list = new ArrayList<>();
    public static int[] count = new int[N];

    public static class Edge {
        public int to;
        public int value;
        public int next;

        public Edge(int to, int value, int next) {
            this.to = to;
            this.value = value;
            this.next = next;
        }
    }

    public static class Point implements Comparable<Point> {
        public int index;

        public Point(int index) {
            this.index = index;
        }

        @Override
        public int compareTo(Point p) {
            return Integer.compare(dist[this.index], dist[p.index]);
        }
    }

    public static void add(int from, int to, int value) {
        list.add(new Edge(to, value, h[from]));
        h[from] = index++;
    }

    public static int spfa(int start, int end, int n) {
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;

        Queue<Point> queue = new PriorityQueue<>();
        queue.add(new Point(start));
        count[start] ++;
        while (!queue.isEmpty()) {
            int t = queue.poll().index;

            for (int j = h[t]; j != -1; j = list.get(j).next) {
                Edge e = list.get(j);
                if (dist[e.to] > dist[t] + e.value) {
                    dist[e.to] = dist[t] + e.value;
                    queue.add(new Point(e.to));
                    count[e.to]++;
                }
                if (count[e.to] >= n) {
                    return -2;
                }
            }
        }

        if (dist[end] == Integer.MAX_VALUE) {
            return -1;
        }
        return 0;
    }

    public static void main(String[] args) {
        Arrays.fill(h, -1);
        Arrays.fill(count, 0);
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();

        while (m-- != 0) {
            int to = scanner.nextInt();
            int from = scanner.nextInt();
            int value = scanner.nextInt();
            add(from, to, value);
        }

        for (int i = 1; i <= n; i++) {
            add(0, i, 0);
        }

        if (spfa(0, n, n) != 0) {
            System.out.println("NO");
            return;
        }

        for (int i = 1; i <= n; i ++) {
            System.out.printf("%d ", dist[i]);
        }
    }
}

种树

题目背景

一条街的一边有几座房子，因为环保原因居民想要在路边种些树。

题目描述

路边的地区被分割成块，并被编号成$1, 2, \ldots,n$。每个部分为一个单位尺寸大小并最多可种一棵树。

每个居民都想在门前种些树，并指定了三个号码$b$，$e$ ，$t$ 。这三个数表示该居民想在地区$b$ 和$e$ 之间（包括$b$ 和$e$）种至少$t$ 棵树。

居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。

输入格式

输入的第一行是一个整数，代表区域的个数$n$。

输入的第二行是一个整数，代表房子个数$h$。

第$3$ 到第$(h + 2)$ 行，每行三个整数，第$(i + 2)$ 行的整数依次为$b_i, e_i, t_i$，代表第$i$ 个居民想在$b_i$ 和$e_i$ 之间种至少$t_i$ 棵树。

输出格式

输出一行一个整数，代表最少的树木个数。

样例 #1

样例输入 #1

9
4
1 4 2
4 6 2
8 9 2
3 5 2

样例输出 #1

5

数据规模与约定

对于$100\%$ 的数据，保证：

-$1 \leq n \leq 3 \times 10^4$，$1 \leq h \leq 5 \times 10^3$。

-$1 \leq b_i \leq e_i \leq n$，$1 \leq t_i \leq e_i - b_i + 1$。

解析

使用前缀和，那么题目给出的条件就可以被转化为 $S[E]−S[B−1] \ge T$ 。但仅仅是这样是不够的，还要注意到，题目要求每一块上只能种一棵树，所以我们有 $0 \le S[i+1]−S[i] \le 1$，以这些约束条件建图求最长路就可以解决了。

例程

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;

public class Main {
    public static final int N = 30010;
    public static int index = 0;
    public static int[] h = new int[N];
    public static int[] dist = new int[N];
    public static List<Edge> list = new ArrayList<>();

    public static class Edge {
        public int to;
        public int value;
        public int next;

        public Edge(int to, int value, int next) {
            this.to = to;
            this.value = value;
            this.next = next;
        }
    }

    public static class Point implements Comparable<Point> {
        public int index;

        public Point(int index) {
            this.index = index;
        }

        @Override
        public int compareTo(Point p) {
            return Integer.compare(dist[p.index], dist[this.index]);
        }
    }

    public static void add(int from, int to, int value) {
        list.add(new Edge(to, value, h[from]));
        h[from] = index++;
    }

    public static void spfa(int start) {
        Arrays.fill(dist, -1);
        dist[start] = 0;

        Queue<Point> queue = new PriorityQueue<>();
        queue.add(new Point(start));
        while (!queue.isEmpty()) {
            int t = queue.poll().index;

            for (int j = h[t]; j != -1; j = list.get(j).next) {
                Edge e = list.get(j);
                if (dist[e.to] < dist[t] + e.value) {
                    dist[e.to] = dist[t] + e.value;
                    queue.add(new Point(e.to));
                }
            }
        }
    }

    public static void main(String[] args) throws IOException {
        Arrays.fill(h, -1);
        Read read = new Read();
        int n = read.nextInt();
        int m = read.nextInt();

        while (m-- != 0) {
            int b = read.nextInt();
            int e = read.nextInt();
            int t = read.nextInt();
            add(b - 1, e, t);
        }
        for (int i = 1; i <= n; i++) {
            add(0, i, 0);
            if (i != n) {
                add(i + 1, i, -1);
                add(i, i + 1, 0);
            }
        }

        spfa(0);
        System.out.println(dist[n]);
    }
}
class Read {
    StreamTokenizer streamTokenizer = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public int nextInt() throws IOException {
        streamTokenizer.nextToken();
        return (int) streamTokenizer.nval;
    }
}