一、欧拉路径
定义
欧拉路径是指从图中任意一个点开始到图中任意一个点结束的路径,并且经过图中每条边,且只经过一次。
存在条件
连通图
对于无向图:
有且只有两个点的度为一,且这两个点分别为起点和终点。
对于有向图:
存在一个点出度比入度多一作为起点,存在一点入度比出度多一作为终点,其余点出度等于入度;否则所有点的出入度必须相等。
二、欧拉回路
定义
起点与终点相同的欧拉路径。
存在条件
连通图
对于无向图:
每个点的度都为偶数。
对于有向图:
每个点的出度等于入度。
三、欧拉回路树(Euler Tours on Trees, ETT)
树(无根树,即没有环的联通无向图)正常情况下没有欧拉回路,但是把每条无向边 $\{u,v\}$ 变为一条 $(u,v)$ 的有向边与一条 $(v,u)$ 的有向边之后,就具有了欧拉回路。
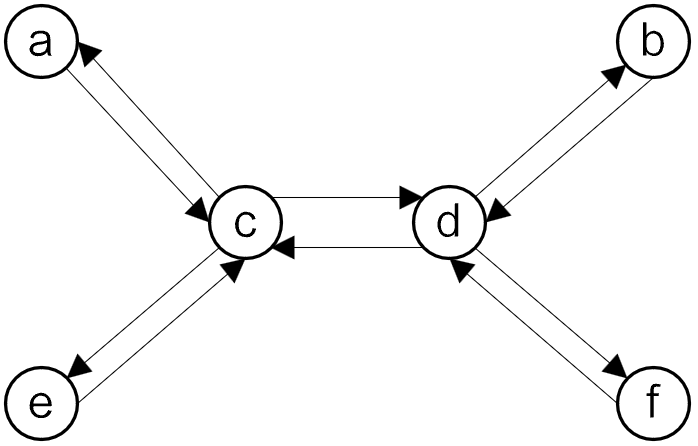
使用这样的方式,就可以将树转化为一条链,长度 $ \le 2n$ 。而维护原来的树,可以转化为维护这个欧拉回路。而维护一条链是相对简单的任务。
